Mastering Quicksort: An Efficient Sorting Algorithm Explained
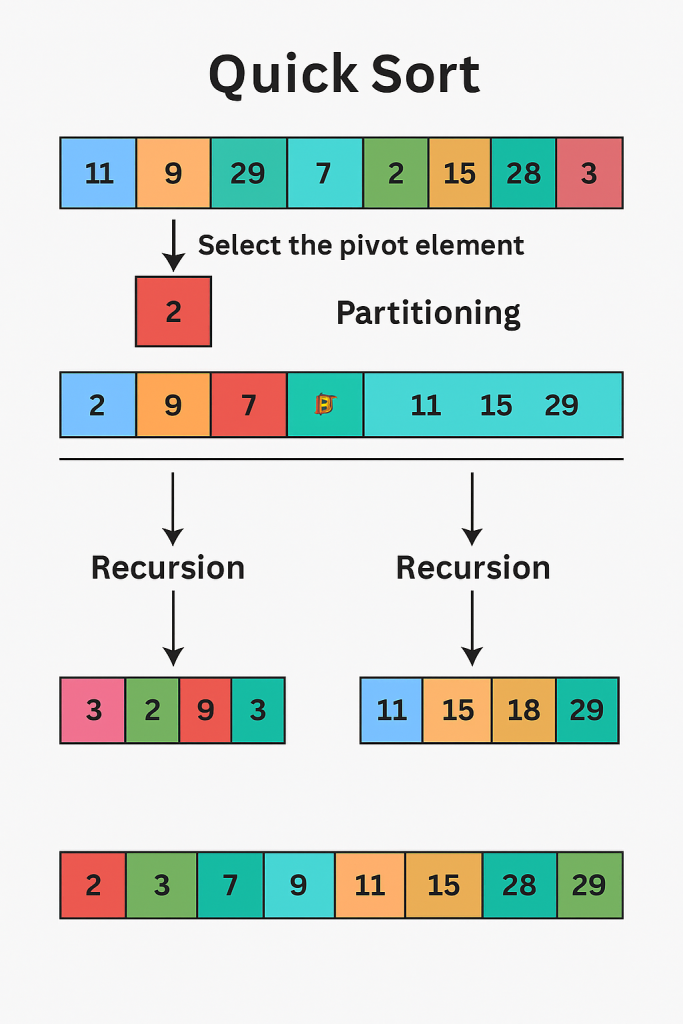
Sorting algorithms are a fundamental concept in computer science, and QuickSort is one of the most efficient and widely used methods. In this article, we’ll explore the QuickSort algorithm, discuss its pseudocode, and provide a Python implementation. By the end, you’ll have a solid understanding of how QuickSort works and how to apply it in your projects.
What is QuickSort?
QuickSort is a divide-and-conquer sorting algorithm developed by Tony Hoare in 1959. It works by selecting a ‘pivot’ element from the array and partitioning the other elements into two sub-arrays based on whether they are less than or greater than the pivot. The sub-arrays are then recursively sorted. This process results in a highly efficient and often faster sorting method compared to other algorithms like Bubble Sort or Insertion Sort.
Pseudocode for QuickSort
Before diving into the Python implementation, let’s take a look at the pseudocode for QuickSort:
Pseudocode
function quicksort(arr)
if length of arr ≤ 1
return arr
select a pivot element from arr
create sub-array less than pivot
create sub-array greater than pivot
return concatenate(quicksort(less than pivot), pivot, quicksort(greater than pivot))Python Implementation of QuickSort
Now that we have an understanding of the pseudocode, let’s translate it into Python code:
def quicksort(arr):
if len(arr) <= 1:
return arr
else:
pivot = arr[len(arr) // 2]
less_than_pivot = [x for x in arr if x < pivot]
equal_to_pivot = [x for x in arr if x == pivot]
greater_than_pivot = [x for x in arr if x > pivot]
return quicksort(less_than_pivot) + equal_to_pivot + quicksort(greater_than_pivot)
# Example usage:
array = [33, 10, 68, 19, 42, 7, 24]
sorted_array = quicksort(array)
print(sorted_array) # Output: [7, 10, 19, 24, 33, 42, 68]Understanding the Code
- Base Case: If the array has one or zero elements, it is already sorted, so we return it.
- Pivot Selection: We select a pivot element. In this example, we chose the middle element of the array.
- Partitioning: We create three sub-arrays: elements less than the pivot, elements equal to the pivot, and elements greater than the pivot.
- Recursive Sorting: We recursively apply QuickSort to the sub-arrays and concatenate the results.
Advantages of QuickSort
- Efficiency: QuickSort has an average-case time complexity of O(n log n), making it faster than many other sorting algorithms.
- In-Place Sorting: It requires only a small amount of additional memory, making it efficient in terms of space.
- Flexibility: QuickSort can be easily adapted and optimized for different types of data and applications.
Conclusion
QuickSort is a powerful and efficient sorting algorithm that is widely used in various applications. By understanding its underlying principles and implementation, you can leverage its benefits in your projects. Try implementing this algorithm in your code and observe the performance improvements it brings to your sorting tasks.